Complete GRE Quantitative Reasoning Syllabus
Preparing for the GRE Quantitative Reasoning section? At MKS Education, we provide a comprehensive syllabus to ensure you’re well-prepared for every type of question. Below is the detailed breakdown of the topics covered in our GRE Quantitative Reasoning classes.
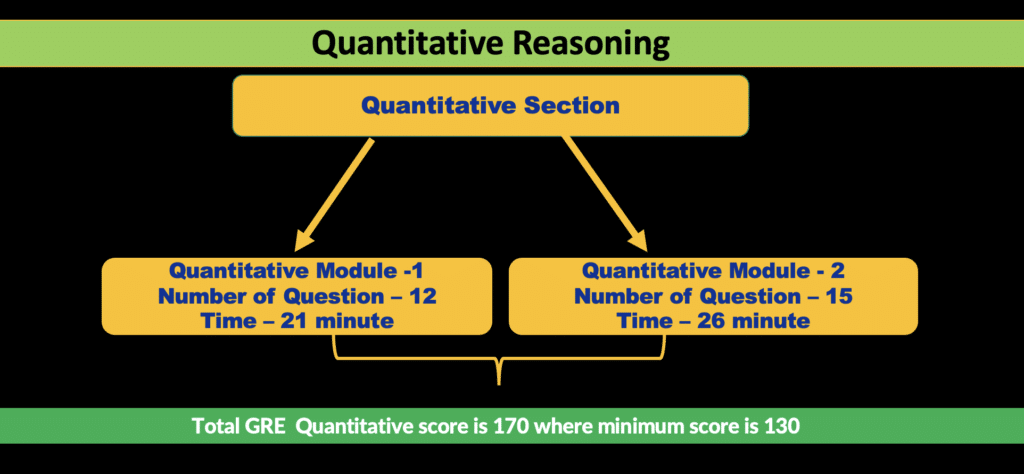
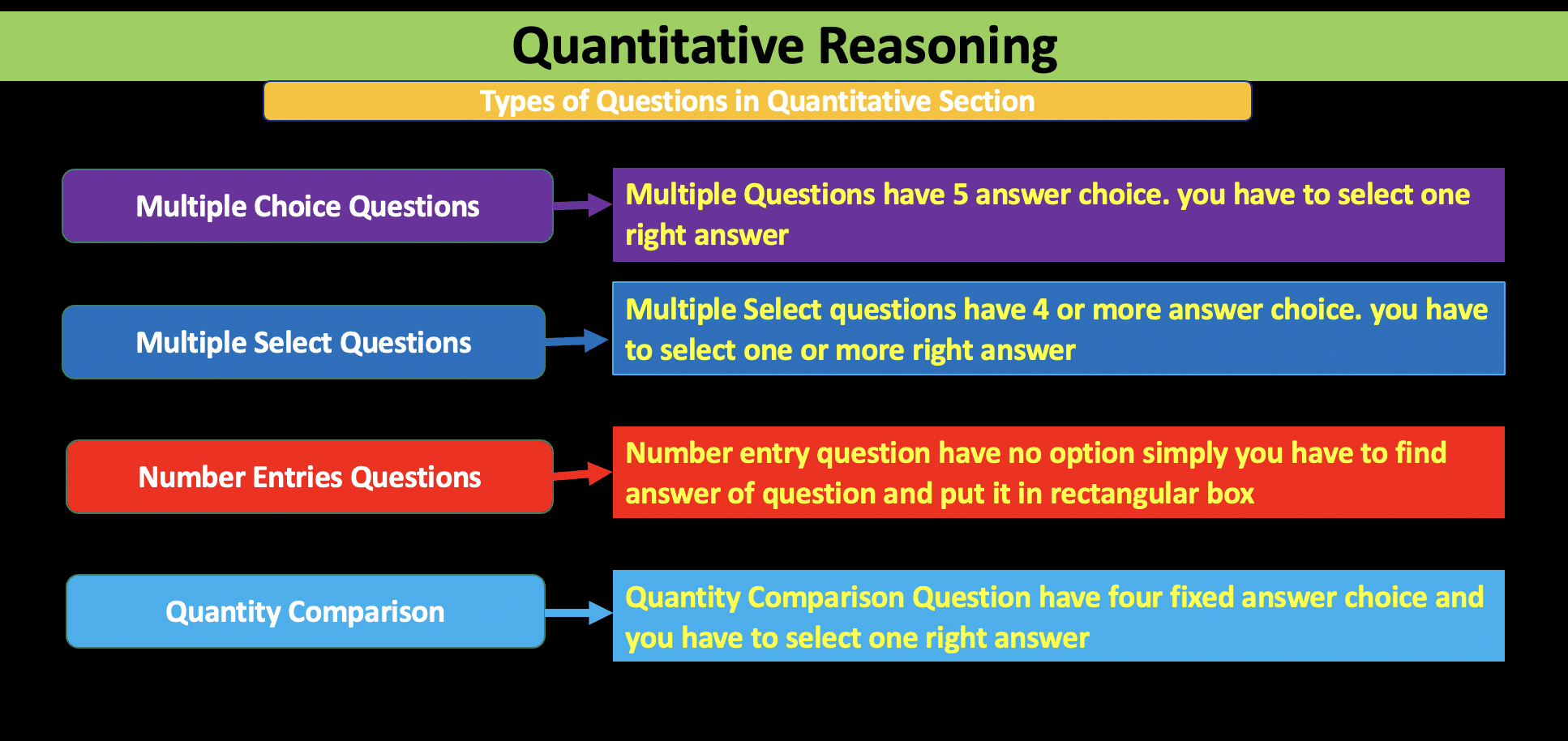
Quantitative Syllabus
I. Number Properties
- Unit Digit
- Odd and Even Numbers
- Integers
- Prime Numbers
- Factors and Multiples
II. Algebra
- Decimals
- Alphanumeric Expressions
- Symbols and Functions
- Progressions (Arithmetic and Geometric)
- Exponents and Roots
- Inequalities and Modulus
- Simplifications and Equations
III. Geometry
- Lines and Angles
- Triangles
- Quadrilaterals
- Circles
- Solid Geometry
- Coordinate Geometry
IV. Advanced Topics
- Permutations and Combinations
- Probability
- Statistics
- Data Analysis
V. Word Problems
- Percentages
- Ratios and Proportions
- Work, Rate, and Time
- Speed, Distance, and Time
- Mixtures and Allegations
- Age and Digit Problems
- Interests and Population Growth
- Sets
At MKS Education, we ensure every topic is covered in-depth with practical examples and strategies to help you solve problems quickly and accurately.
Also, Visit GRE Free Resources
Numer Property
1. Unit Digit
Understanding the unit digit is crucial for solving problems involving large numbers, patterns, or cyclic repetition. This topic focuses on identifying the last digit of a number after various operations, such as multiplication or exponentiation. It’s particularly useful for quickly solving problems where exact calculations are unnecessary. By mastering this, students can save time and improve accuracy on the GRE.
2. Odd and Even Numbers
Odd and even numbers form the foundation of number properties. This topic explores their basic definitions, operations, and rules, such as how the sum, difference, or product of odd and even numbers behaves. It also dives into identifying patterns in sequences and solving problems that test these properties in algebraic or real-world scenarios.
3. Integers
Integers encompass whole numbers, both positive and negative, including zero. This topic teaches students to work with the properties of integers, including divisibility rules, operations, and their applications in equations and inequalities. Understanding integers is vital for solving problems that involve number lines, sequences, or discrete values.
4. Prime Numbers
Prime numbers are a key concept in GRE Quantitative Reasoning. This topic covers the definition of primes, their properties, and their role in factorization and divisibility. Students learn to identify prime numbers, apply the prime factorization method, and solve problems involving greatest common divisors (GCD) and least common multiples (LCM).
5. Factors and Multiples
Factors and multiples form the basis for understanding divisibility and solving complex word problems. This topic focuses on identifying the factors of a number, finding common factors or multiples, and understanding the relationship between numbers. Key applications include solving problems involving ratios, proportions, and number patterns.
Algebra
6. Decimals
Decimals are critical for solving problems involving precision and fractional values. This topic focuses on operations with decimals, including addition, subtraction, multiplication, and division. Students also learn to convert between fractions and decimals, compare decimal values, and apply these concepts in real-world scenarios, such as currency calculations or measurement problems.
7. Alphanumeric Expressions
Alphanumeric expressions combine numbers and letters to represent mathematical relationships. This topic teaches students to interpret and simplify expressions involving variables and constants. Understanding alphanumeric expressions is essential for solving equations, inequalities, and word problems that require translating verbal statements into mathematical form.
8. Symbols and Functions
Symbols and functions introduce students to abstract representations of mathematical relationships. This topic includes interpreting custom symbols, understanding domain and range, and solving problems involving basic and complex functions. GRE questions often test students’ ability to work with unfamiliar symbols and quickly identify the rules governing them.
9. Progressions (Arithmetic and Geometric)
Progressions cover sequences of numbers that follow specific patterns. Students learn to identify arithmetic progressions (constant difference) and geometric progressions (constant ratio). This topic includes finding the nth term, calculating sums, and solving problems related to patterns, series, and practical applications, such as population growth or financial calculations.
10. Exponents and Roots
Exponents and roots form the backbone of algebraic problem-solving. This topic covers the laws of exponents, properties of square roots, and higher-order roots. Students also learn to simplify complex expressions, solve equations involving powers, and handle problems that test their understanding of exponential growth or decay.
11. Inequalities and Modulus
Inequalities and modulus teach students to work with non-equal relationships and absolute values. This topic includes solving linear and quadratic inequalities, graphing solutions, and understanding the behavior of absolute values. These concepts are critical for analyzing ranges, boundaries, and relationships between variables.
12. Simplifications and Equations
Simplifications and equations focus on reducing complex algebraic expressions and solving linear or quadratic equations. This topic teaches students to identify key relationships, factorize polynomials, and apply strategies for solving multi-variable equations. Mastery of this topic is crucial for tackling word problems and data interpretation questions.
Geometry
13. Lines and Angles
Lines and angles are the foundation of geometry. This topic covers the properties of lines, such as parallel, perpendicular, and intersecting lines, as well as the types of angles, including acute, obtuse, and right angles. Students learn the relationships between angles, such as complementary and supplementary angles, and how to solve problems involving angle measurements in geometric diagrams.
14. Triangles
Triangles are one of the most important shapes in geometry. This topic includes the properties of different types of triangles (equilateral, isosceles, and scalene), the Pythagorean theorem, and triangle inequality. Students also learn about special right triangles, such as 30-60-90 and 45-45-90 triangles, and how to calculate area, perimeter, and angles.
15. Quadrilaterals
Quadrilaterals include four-sided polygons such as squares, rectangles, parallelograms, and trapezoids. This topic focuses on the properties of these shapes, including their sides, angles, and diagonals. Students learn to calculate areas, perimeters, and other measurements, as well as solve problems involving relationships between different quadrilaterals.
16. Circles
Circles involve a unique set of properties and formulas. This topic covers the definitions of radius, diameter, chord, arc, and tangent, as well as key formulas for circumference and area. Students learn to solve problems involving sectors, central angles, and inscribed angles, and apply these concepts in real-world contexts.
17. Solid Geometry
Solid geometry extends two-dimensional concepts into three dimensions. This topic includes the properties of common solids, such as cubes, cylinders, spheres, cones, and rectangular prisms. Students learn to calculate surface area, volume, and diagonal lengths, and solve problems that test spatial reasoning and visualization.
18. Coordinate Geometry
Coordinate geometry combines algebra and geometry to solve problems on the Cartesian plane. This topic covers plotting points, finding distances and midpoints, and understanding the slope and equation of a line. Students also learn about parabolas, circles, and other shapes in a coordinate system, enabling them to solve complex problems efficiently.
Advanced Topic
19. Permutations and Combinations
Permutations and combinations focus on counting principles used to solve problems involving arrangements and selections. This topic teaches students to distinguish between situations where order matters (permutations) and where it doesn’t (combinations). Key concepts include factorials, the combination formula, and practical applications like arranging items or forming groups.
20. Probability
Probability is the study of chance and uncertainty. This topic covers fundamental concepts such as calculating the likelihood of single or multiple events, independent and dependent events, and the complement rule. Students learn to analyze scenarios and solve problems related to real-world situations like games, experiments, or predictions.
21. Statistics
Statistics involves understanding and interpreting data. This topic includes measures of central tendency (mean, median, and mode), measures of dispersion (range, variance, and standard deviation), and interpreting data presented in graphs or tables. Students also learn how to identify trends, compare datasets, and apply statistical reasoning in problem-solving.
22. Data Analysis
Data analysis builds on statistical concepts to interpret and solve complex problems using visual and numerical data. This topic covers understanding bar graphs, pie charts, histograms, and scatterplots. Students also learn how to extract insights, calculate percentages, and make data-driven conclusions, which are often tested in GRE Quantitative questions.
Word Problem
23. Percentage
Percentage problems focus on understanding and calculating proportions expressed as parts of 100. This topic includes finding percentages, percentage increase or decrease, and solving problems related to discounts, markups, and profit margins. Students learn to apply these concepts in real-world scenarios, such as financial analysis and population studies.
24. Ratio and Proportion
Ratios and proportions involve comparing quantities and maintaining equivalency between relationships. This topic includes solving problems related to direct and inverse proportions, scaling, and dividing quantities in given ratios. These concepts are essential for solving questions in areas such as mixtures, rates, and geometry.
25. Work, Rate, and Time
This topic explores the relationship between work, rate, and time, focusing on efficiency and productivity. Students learn to solve problems involving multiple workers, machines, or processes working together or independently. These problems often require logical thinking and a clear understanding of proportional reasoning.
26. Speed, Distance, and Time
Speed, distance, and time problems involve motion and movement. This topic includes concepts such as average speed, relative speed, and problems involving objects moving in opposite or the same direction. Students also learn to handle complex scenarios involving multiple moving objects or varying speeds.
27. Mixtures and Alligation
Mixture and alligation problems deal with combining substances or groups with different properties to achieve a desired result. This topic teaches students to calculate concentrations, proportions, or costs in mixture problems, often using the alligation rule for faster solutions. These problems are commonly seen in contexts like blending products or preparing solutions.
28. Age and Digit Problems
Age and digit problems involve reasoning with unknown quantities related to ages or numbers. Students learn to form and solve equations based on relationships between individuals’ ages or the properties of numerical digits, such as sums or reversals. These problems test logical thinking and algebraic skills.
29. Interest and Population Growth
This topic covers concepts of simple and compound interest, as well as growth models for populations or investments. Students learn to calculate interest over varying time periods, apply formulas, and interpret growth patterns. These concepts are crucial for financial and economic problem-solving on the GRE.
30. Sets
Set theory involves understanding and working with groups of items that share common properties. This topic includes union, intersection, Venn diagrams, and solving problems with overlapping sets. Students also learn to calculate the number of elements in combined sets using formulas and logical reasoning.
👁👁 Views: 1000136
